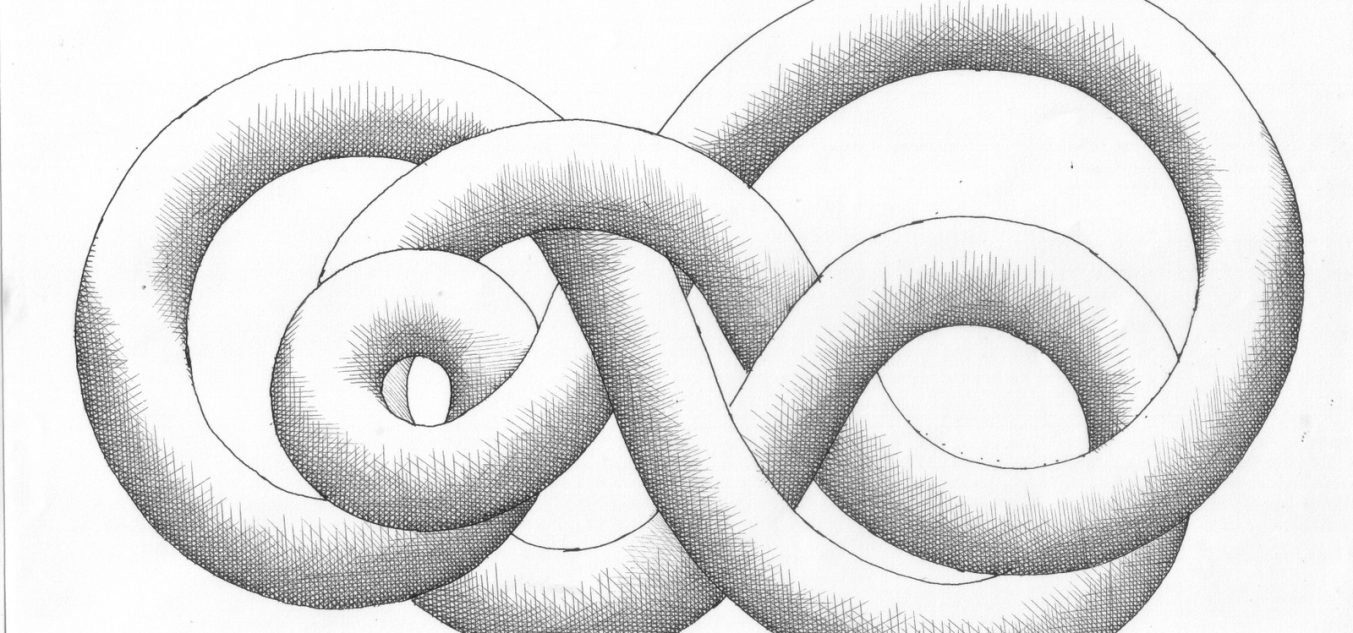
Une boucle fermée. Si on tire sur les extrémités, obtient-on un nœud ou pas ?
La topologie est l’étude des propriétés invariantes dans la déformation géométrique des objets et dans les transformations continues appliquées à des êtres mathématiques.
La théorie des nœuds est une branche de la topologie qui consiste en l’étude mathématique de courbes présentant des liaisons avec elles-mêmes, un « bout de ficelle » idéalisé en lacets. La théorie des nœuds a commencé vers 1860 avec des travaux de Carl Friedrich Gauss liés à l’électromagnétisme.
Nous y voilà.
La théorie des nœuds est très proche de la théorie des tresses qui comporte plusieurs chemins ou « bouts de ficelle ». Les tresses ont une structure de groupe naturelle, et possèdent des liens profonds avec des domaines divers des mathématiques notamment en topologie, théorie des nœuds et combinatoire algébrique. Cette théorie trouve des applications en physique statistique, en mécanique quantique ainsi qu’en informatique théorique, par exemple en cryptographie.
Caractéristiques
Encre sur papier, juin 2013, A4